Capabilities
Capabilities
Uncertainty Quantification in Computational Models of Physical Systems
Laboratory
Sandia National Laboratories (SNL)Capability Expert
Bert J. Debusschere, Habib N. NajmClass
AnalysisComputational Tools and Modeling
Node Readiness Category
2: High-Temperature Electrolysis (HTE)2: Low-Temperature Electrolysis (LTE)
2: Photoelectrochemical (PEC)
1: Solar Thermochemical (STCH)
Description
Sandia National Laboratories has extensive expertise in the development of uncertainty quantification (UQ) methods and software, and their use in assessing confidence in physical system model predictions as well as model selection based on data and expert knowledge. This capability has evolved over nearly two decades and is not otherwise available commercially. We routinely implement UQ methods in our UQ Toolkit (UQTk) software library, which is available as open-source software under the Modified BSD license. UQTk offers methods for propagating input uncertainties through computational models, for sensitivity analysis, and for Bayesian calibration and parameter estimation based on experimental data. One of the key features of UQTk is that it offers its capabilities as modular tools that can be strung together to form a full UQ workflow with all required steps to go from experimental data analysis to model output uncertainty assessment. We have used UQTk capabilities for UQ studies in numerous applications, including Hydrogen conversion processes, modeling of hydrocarbon fuel chemistry, electrochemistry in microfluidic systems, turbulent combustion, climate modeling, electric power grid optimization, modeling of materials equation of state, and material damage in nuclear fusion.
In the context of Hydrogen conversion processes, we have used Bayesian methods in UQTk to assess the accuracy of thermodynamic models for redox-active materials such as Ceria, and to propagate the associated model errors into derived quantities such as enthalpy changes and process efficiencies. This assessment makes it possible to evaluate the trade-off between model complexity, computational cost, input data accuracy, and confidence in the overall process efficiency. In a similar context, we are currently refining automated approaches to select the most relevant terms in the Compound Energy Framework for redox-active materials when fitting against DFT and TGA data. This work builds on novel approaches developed by our ASU collaborators [Wilson, S. A., Stechel, E. B., & Muhich, C. L. (2022)] and adds a more rigorous numerical and UQ analysis to the process. In the broader HydroGen AWSM context, predictions with quantified uncertainty are well suited for informed decision support strategies given uncertain scenarios, such as, e.g. the analysis of credible paths towards commercialization using techno-economic analysis.
Capability Bounds
Methods are challenged in situations when dealing with complex models with large numbers of uncertain parameters. Further, while the methods are quite general, their utilization in particular physical systems often involves a degree of customization for maximal performance effectiveness. Accordingly, we envision potential further development of methods and UQTk software targeted at relevant AWSM problems.
Unique Aspects
Our UQ group brings together a unique critical mass of expertise in engineering and applied math that is unparalleled across the labs, with an established pedigree and recognizable brand in the international UQ community. Our UQTk software provides a unique assortment of a wide range of practically motivated UQ methods, with an international group of users and under continual active development.
Availability
Our UQ team is actively engaged in collaborations across the DOE lab complex and academia. We regularly engage with other groups in collaborative research projects/visits. We also frequently offer tutorials on UQ methods in general as well as on the use of UQTk particularly.
Benefit
UQ enables the assessment of uncertainty in system predictions, thereby providing means for robust design optimization, qualification of design performance, and means for the use of predictions for decision support. Further, it would provide well-founded means for hypothesis testing and model selection/validation in the context of sparse and noisy data.
Images

Left frame: Uncertainty in thermodynamic equations of state for Aluminum [1]. Bayesian inference was used to infer the equation of state parameters from experimental data, allowing its use for UQ in shock hydrodynamics codes. The graph shows the marginal and joint posterior distributions of the equation of state parameters that were inferred from experimental data.
Right frame: Large eddy simulations of turbulent combustion in a bluff body burner [2]. UQTk was used for forward propagation of uncertainty in this system, accounting for uncertainty in subgrid model parameters, and allowing inspection of the contribution of different processes to uncertainty in predicted quantities of interest.
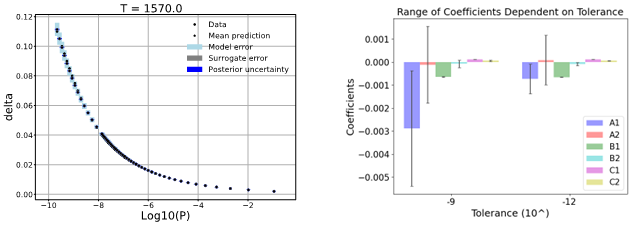
Left frame: Fit of a model for Oxygen deficiency d in Ceria as a function of Oxygen pressure at T = 1570K, based on data from [Zinkevich, et al., 2006]. The Bayesian Inference approach in UQTk provides the uncertainty in the fit due to the model structure (Model Error), the amount of data available (Posterior Uncertainty), and the approximation of the full model by a surrogate model (Surrogate Error).
Right frame: Analysis of how the coefficients of the end member terms in a Compound Energy Formulation of a redox-active material depend on the tolerance used in the regression approach. For tolerances in the nonlinear solver of 10-12 and better, all terms are accurately determined. The A terms are correction terms with neglible impact on the fit quality for this particular case, which is why they are not well-defined.
References
1. A.C. Robinson, R.D. Berry, J.H. Carpenter, B. Debusschere, R.R. Drake, A.E. Mattsson, and W.J. Rider, "Fundamental issues in the representation and propagation of uncertain equation of state information in shock hydrodynamics", Computers & Fluids, 83: 187-193, 2013.
2. M. Khalil, G. Lacaze, J.C. Oefelein, and H.N. Najm, "Uncertainty Quantification in LES of a Turbulent Bluff-body Stabilized Flame", Proc. Comb. Inst., 35:1147-1156, 2015.
Website: http://www.sandia.gov/uqtoolkit
